Navigatie
- Hoe navigeren we op Trui?
- Rekenen aan het getij
- Twaalfde-regel
- Rekenvoorbeelden
- Automatische Getij Tool
- Nieuwtjes
Het Varen
Het IJsselmeer
Het Markermeer
De Randmeren
Friesland
Het Wad
- Het Nederlandse Wad
- Het Oost-Friese Wad
- Tussen Jade en Elbe
- Het Wad van Dithmarschen
- Het Noord-Friese Wad
- Kroegen aan de Nederlandse Waddenzee
- Kroegen in Ostfriesland
- Kroegen in Nordfriesland
- De regels in Duitsland
Zeeland
De Oostzee
De staande mast route
Twaalfde-regel
Dit is een manier om de sinus van het tij te benaderen. We verdelen hiertoe de vloed of eb in zes uren. Het tijverschil verdelen we in twaalf gelijke delen, zie onderstaande grafiek.
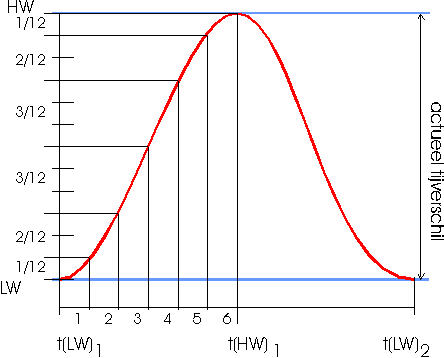
We benaderen de sinus nu als volgt:
| uur | toename | totaal |
|---|---|---|
| 1 | 1/12 | 1/12 |
| 2 | 2/12 | 3/12 |
| 3 | 3/12 | 6/12 |
| 4 | 3/12 | 9/12 |
| 5 | 2/12 | 11/12 |
| 6 | 1/12 | 12/12 |
Complicatie
Heel leuk allemaal, maar het Wad zou het Wad niet zijn als er geen complicatie was die de argeloze zeiler genadeloos verneukt. Nabij Harlingen vraagt de schipper aan sio1 en aan sio2 tot welk tijdstip we over een bepaalde plaat kunnen. Beide gaan rekenen. Beide concluderen dat het met half tij (6/12) nog precies kan. Sio1 meldt zich bij de schipper en zegt dat de botter uiterlijk half twee over de plaat moet. Sio2 komt er bij staan en zegt dat we tot drie uur de tijd hebben. Een flauwe glimlach speelt rond de lippen van de schipper, hij denkt terug aan de tijd dat hij nog sio was, en zich door hetzelfde verschijnsel liet verneuken...
De oplossing van het raadsel zit hem in de asymmetrie van het tij. Sio1 heeft gerekend dat tot drie uur na hoog er genoeg water staat. Sio2 daarentegen is er vanuit gegaan dat tot drie uur voor laag genoeg water is. En die twee dingen zijn bepaald niet hetzelfde! Bij Harlingen duurt, door de bank genomen, de vloed 5 uur, en eb 7,5 uur. Dit verklaart het verschil van 1,5 uur tussen de uitkomsten van beide sio's.
Hoe lossen we dit op? Heel eenvoudig: we passen de lengte van de uren aan. In dit geval rekenen we bij vloed met uren van 50 minuten, bij eb met uren van 75 minuten. Dan klopt de benadering weer. Heb je te maken met een tij waarbij vloed 5,5 uur duurt, en eb 7, dan reken je met uren van 55 respectievelijk 70 minuten.